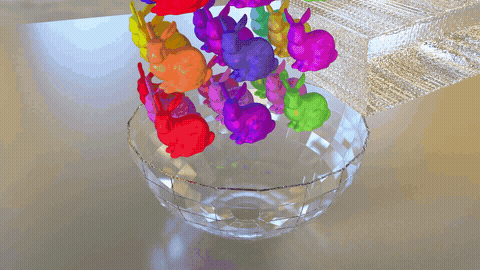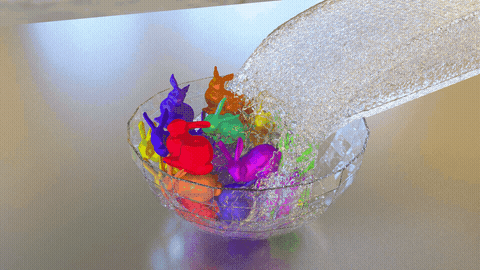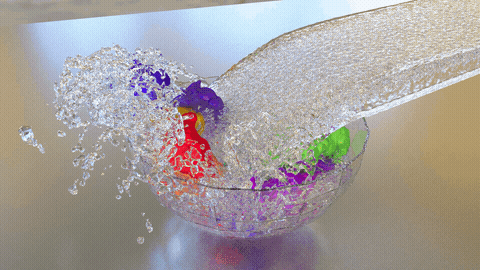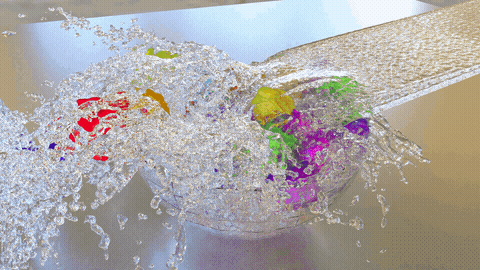publications
You can also find the updated list of publications on my Google Scholar profile.
2026
- The virtual stress boundary method to impose nonconforming Neumann boundary conditions in the high‐order material point methodYong Liang, Joel Given, Bodhinanda Chandra, and 3 more authorsInternational Journal for Numerical Methods in Engineering, Mar 2026
Previous studies have demonstrated that the virtual stress boundary (VSB) method accurately and efficiently imposes nonconforming Neumann boundary conditions in the material point method (MPM). A key advantage of the VSB method is its ability to impose boundary conditions without requiring explicit knowledge of the boundary’s position. This is achieved through a transformation that replaces the original boundary traction with an equivalent virtual stress field. The inclusion of this virtual stress field allows the governing equations to be solved using only volume integrals, which are easily computed in the MPM using a particle‐wise quadrature scheme. In this study, the VSB method is extended to accommodate various high‐order MPM variations. The updates mainly involve addressing the non‐local support domain of high‐order shape functions and enhancing quadrature accuracy in filled cells. The accuracy and versatility of the combined high‐order MPM and VSB method are demonstrated through numerical examples in 1D, 2D, and 3D.
@article{Liang2026, author = {Liang, Yong and Given, Joel and Chandra, Bodhinanda and Zeng, Zhixin and Zhang, Xiong and Soga, Kenichi}, doi = {10.1002/nme.70291}, issn = {0029-5981}, issue = {5}, journal = {International Journal for Numerical Methods in Engineering}, month = mar, title = {The virtual stress boundary method to impose nonconforming Neumann boundary conditions in the high‐order material point method}, volume = {127}, url = {https://onlinelibrary.wiley.com/doi/10.1002/nme.70291}, year = {2026}, }
2025
- An elasto-viscoplastic thixotropic model for fresh concrete capturing flow-rest transitionJidu Yu, Bodhinanda Chandra, Christopher Wilkes, and 2 more authorsMar 2025
The flow properties of fresh concrete are critical in the construction industry, as they directly affect casting quality and the durability of the final structure. Although non-Newtonian fluid models, such as the Bingham model, are widely used to model these flow properties, they often fail to capture key phenomena, including flow stoppage, and frequently rely on non-physical regularization or stabilization techniques to mitigate numerical instabilities at low shear rates. To address these limitations, this study proposes an elasto-viscoplastic constitutive model within the continuum mechanics framework, which treats fresh concrete as a solid-like material with a rate-dependent yield stress. The model inherently captures the transition from elastic response to viscous flow following Bingham rheology, and vice versa, enabling accurate prediction of flow cessation without ad-hoc criteria. Additionally, a thixotropy evolution law is incorporated to account for the time-dependent behavior resulting from physical flocculation and shear-induced deflocculation. The proposed model is implemented within the Material Point Method (MPM), whose Lagrangian formulation facilitates tracking of history-dependent variables and robust simulation of large deformation flows. Numerical examples demonstrate the model’s effectiveness in reproducing a range of typical concrete flow scenarios, offering a more physically consistent numerical tool for optimizing concrete construction processes and minimizing defects.
@misc{Yu2025, title = {An elasto-viscoplastic thixotropic model for fresh concrete capturing flow-rest transition}, author = {Yu, Jidu and Chandra, Bodhinanda and Wilkes, Christopher and Zhao, Jidong and Soga, Kenichi}, year = {2025}, eprint = {2512.23364}, archiveprefix = {arXiv}, primaryclass = {cond-mat.soft}, url = {https://arxiv.org/abs/2512.23364}, doi = {https://doi.org/10.48550/arXiv.2512.23364}, } - A total-Lagrangian material point method for fast and stable hydromechanical modeling of porous mediaWeijian Liang, Bodhinanda Chandra, Jidu Yu, and 2 more authorsInternational Journal for Numerical Methods in Engineering, Mar 2025
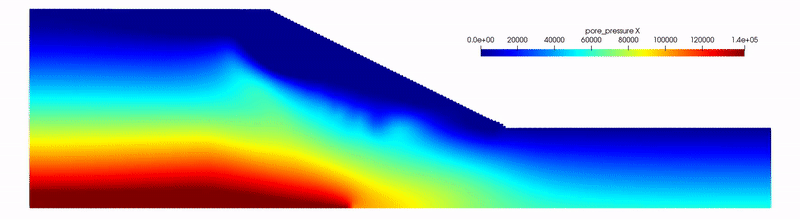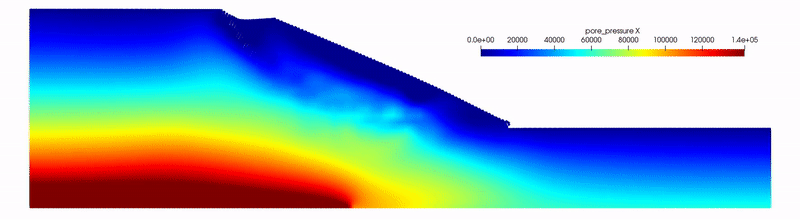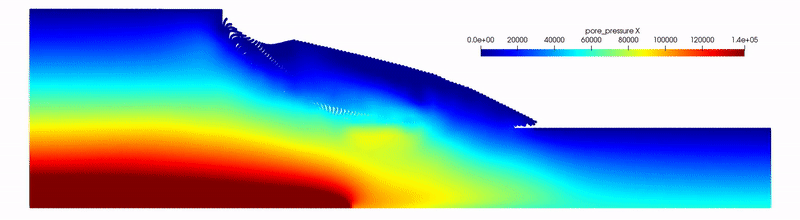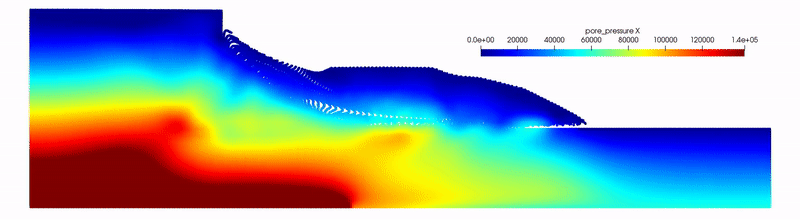
Modeling the incompressible fluid flow in porous media has long been a challenging task in the Material Point Method (MPM). Although widely used, conventional Updated Lagrangian MPM (ULMPM) often suffers from numerical stability and computational efficiency issues in the hydromechanical analysis of saturated porous media. To address these issues, we herein present a novel semi-implicit Total Lagrangian MPM (TLMPM). The proposed TLMPM leverages the fractional step method to decouple pore pressure from kinematic fields and employs the semi-implicit scheme to bypass the small time step constraint imposed by permeability and fluid compressibility. Unlike its UL counterpart, the TLMPM evaluates weighting functions and their gradients only once in the reference configuration, eliminating material point tracking and inherently resolving cell-crossing instabilities. Given the consistent set of active degrees of freedom throughout simulations, the proposed method greatly reduces computational costs associated with system matrix assembly for both kinematics and pore pressure and with free-surface node detection. Furthermore, this feature also facilitates the efficient Cholesky factorization, resulting in a substantial acceleration of the solver performance. The proposed approach has been validated against various benchmark tests, and our results have highlighted the remarkable performance of TLMPM, which can achieve up to 63 times speedup over conventional methods, scaling favorably with problem size, and retaining numerical stability even with low-order basis functions. These advancements position the TLMPM as a transformative tool for poroelastic analysis, with broader applicability to large-deformation problems in geomechanics, energy systems, and environmental engineering.
@article{Liang2025, title = {A total-Lagrangian material point method for fast and stable hydromechanical modeling of porous media}, author = {Liang, Weijian and Chandra, Bodhinanda and Yu, Jidu and Yin, Zhen-Yu and Zhao, Jidong}, journal = {International Journal for Numerical Methods in Engineering}, volume = {126}, number = {19}, pages = {e70135}, year = {2025}, doi = {https://doi.org/10.1002/nme.70135}, url = {https://onlinelibrary.wiley.com/doi/abs/10.1002/nme.70135}, keywords = {fractional step method, incompressible fluid flow, material point method (MPM), porous media, Total Lagrangian}, publisher = {Wiley Online Library} } - Absorbing boundary conditions in material point method adopting perfectly matched layer theoryJun Kurima, Bodhinanda Chandra, and Kenichi SogaSoil Dynamics and Earthquake Engineering, Mar 2025
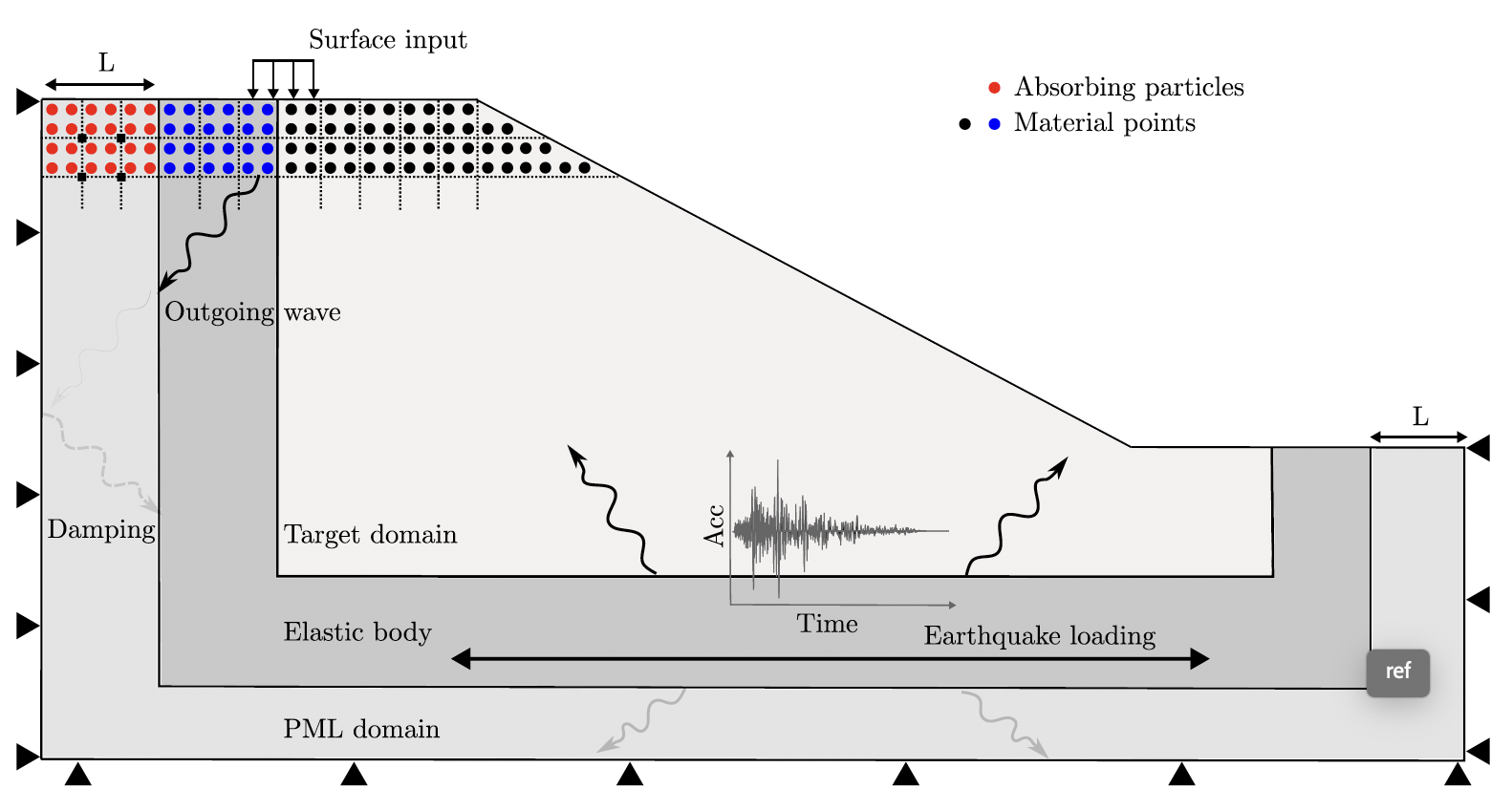
This study focuses on solving the numerical challenges of imposing absorbing boundary conditions for dynamic simulations in the material point method (MPM). To attenuate elastic waves leaving the computational domain, the current work integrates the Perfectly Matched Layer (PML) theory into the implicit MPM framework. The proposed approach introduces absorbing particles surrounding the computational domain that efficiently absorb outgoing waves and reduce reflections, allowing for accurate modeling of wave propagation and its further impact on geotechnical slope stability analysis. The study also includes several benchmark tests to validate the effectiveness of the proposed method, such as several types of impulse loading and symmetric and asymmetric base shaking. The conducted numerical tests also demonstrate the ability to handle large deformation problems, including the failure of elasto-plastic soils under gravity and dynamic excitations. The findings extend the capability of MPM in simulating continuous analysis of earthquake-induced landslides, from shaking to failure.
@article{Kurima2025, title = {Absorbing boundary conditions in material point method adopting perfectly matched layer theory}, journal = {Soil Dynamics and Earthquake Engineering}, volume = {191}, pages = {109219}, year = {2025}, issn = {0267-7261}, doi = {https://doi.org/10.1016/j.soildyn.2025.109219}, url = {https://www.sciencedirect.com/science/article/pii/S0267726125000120}, author = {Kurima, Jun and Chandra, Bodhinanda and Soga, Kenichi}, keywords = {Material point method, Perfectly matched layer, Absorbing boundary, Dynamic analysis, Slope stability, Earthquake-induced landslides} }
2024
- Mixed material point method formulation, stabilization, and validation for a unified analysis of free-surface and seepage flowBodhinanda Chandra, Ryota Hashimoto, Ken Kamrin, and 1 more authorJournal of Computational Physics, Mar 2024
This paper presents a novel stabilized mixed material point method (MPM) designed for the unified modeling of free-surface and seepage flow. The unified formulation integrates the Navier-Stokes equation with the Darcy-Brinkman-Forchheimer equation, effectively capturing flows in both non-porous and porous domains. In contrast to the conventional Eulerian computational fluid dynamics (CFD) solver, which solves the velocity and pressure fields as unknown variables, the proposed method employs a monolithic displacement-pressure formulation adopted from the mixed-form updated-Lagrangian finite element method (FEM). To satisfy the discrete inf-sup stability condition, a stabilization strategy based on the variational multiscale method (VMS) is derived and integrated into the proposed formulation. Another distinctive feature is the implementation of blurred interfaces, which facilitate a seamless and stable transition of flows between free and porous domains, as well as across two distinct porous media. The efficacy of the proposed formulation is verified and validated through several benchmark cases in 1D, 2D, and 3D scenarios. Conducted numerical examples demonstrate enhanced accuracy and stability compared to analytical, experimental, and other numerical solutions.
@article{Chandra2024b, title = {Mixed material point method formulation, stabilization, and validation for a unified analysis of free-surface and seepage flow}, journal = {Journal of Computational Physics}, pages = {113457}, year = {2024}, issn = {0021-9991}, doi = {https://doi.org/10.1016/j.jcp.2024.113457}, url = {https://www.sciencedirect.com/science/article/pii/S0021999124007058}, author = {Chandra, Bodhinanda and Hashimoto, Ryota and Kamrin, Ken and Soga, Kenichi}, keywords = {Material point method, Stabilized methods, Mixed formulation, Navier–Stokes/Darcy–Brinkman–Forchheimer coupling, Blurred interface, Flow in porous media} } - Stabilized mixed material point method for incompressible fluid flow analysisBodhinanda Chandra, Ryota Hashimoto, Shinnosuke Matsumi, and 2 more authorsComputer Methods in Applied Mechanics and Engineering, Mar 2024
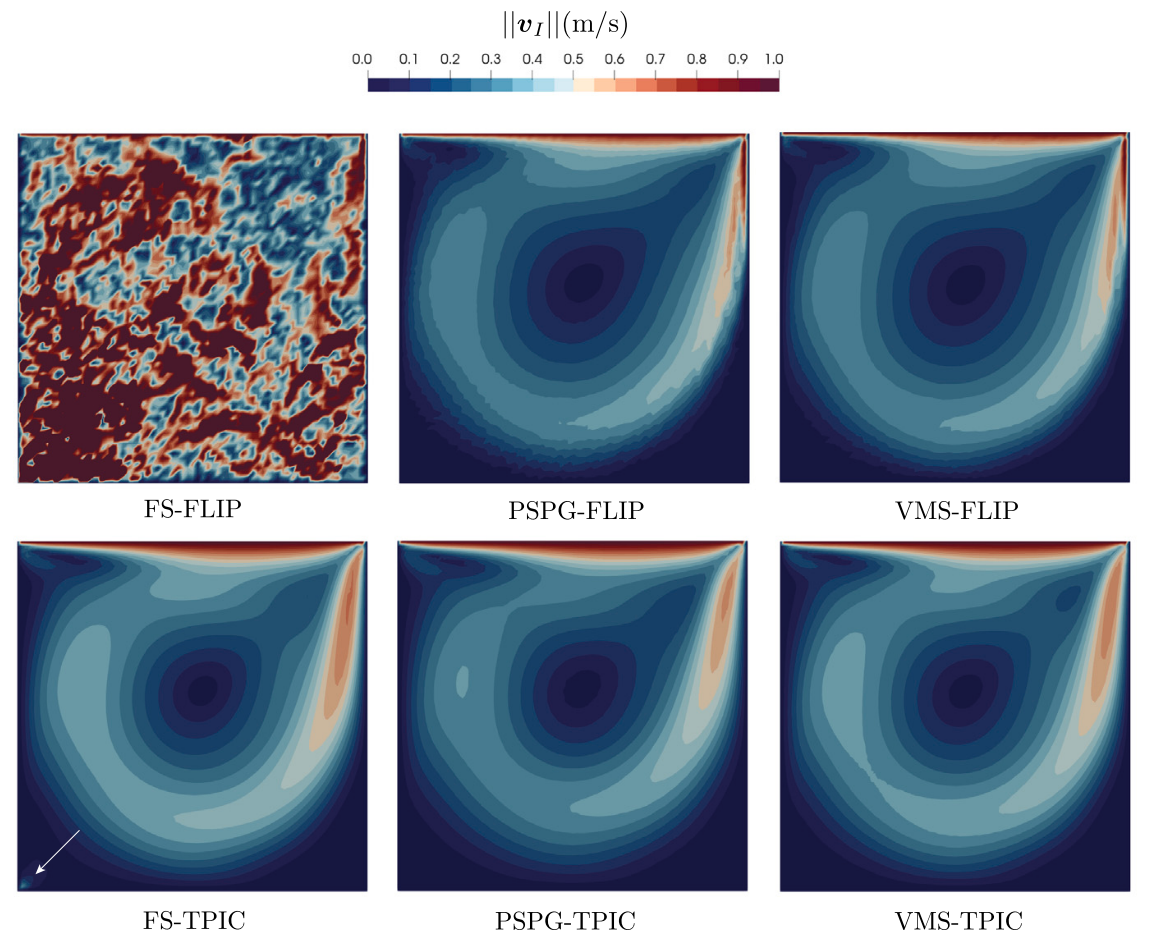
This paper proposes novel and robust stabilization strategies for accurately modeling incom- pressible fluid flow problems in the material point method (MPM). To address the modeling of Newtonian fluids with incompressibility constraints, a new mixed implicit MPM formulation is proposed. Here, instead of solving the velocity and pressure fields as the unknown variables like the typical Eulerian computational fluid dynamics (CFD) solver, the proposed approach adopts a monolithic displacement–pressure formulation inspired by the mixed-form updated- Lagrangian Finite Element Method (FEM). To satisfy the inf–sup stability condition, two stabilization strategies are integrated into the formulation: the variational multiscale method (VMS) and the pressure-stabilization Petrov–Galerkin method (PSPG). By concurrently solving the displacement and pressure fields, the developed monolithic solver obviates the need for free-surface detection as well as Dirichlet and Neumann pressure imposition, in contrast to the fractional-step method. This attribute mitigates spurious pressure and velocity oscillations in simulating dynamic and transient flow problems. This study also addresses other prevalent challenges in MPM simulations, such as the pressure oscillations triggered by cell-crossing errors, particle-distribution-induced quadrature errors, and particle-grid information transfer. To resolve these issues, the quadratic B-Spline basis function, the delta-correction method, and the Taylor particle-in-cell method are incorporated into the proposed mixed MPM formulation, thereby enhancing numerical stability. The efficacy of the proposed stabilized incompressible MPM framework is validated through several benchmark cases, comparing the obtained results with other numerical methods and analytical solutions. Furthermore, the method’s capability in simulating real-world problems involving violent free-surface fluid motion is demonstrated through comparisons with experimental results of water sloshing and dam break scenarios.
@article{Chandra2024, author = {Chandra, Bodhinanda and Hashimoto, Ryota and Matsumi, Shinnosuke and Kamrin, Ken and Soga, Kenichi}, doi = {10.1016/j.cma.2023.116644}, issn = {00457825}, journal = {Computer Methods in Applied Mechanics and Engineering}, pages = {116644}, title = {{Stabilized mixed material point method for incompressible fluid flow analysis}}, url = {https://linkinghub.elsevier.com/retrieve/pii/S0045782523007673}, volume = {419}, year = {2024}, }
2023
- On the derivation of a component-free scheme for Lagrangian fluid–structure interaction problemsMiguel Molinos, Bodhinanda Chandra, Miguel M Stickle, and 1 more authorActa Mechanica, Mar 2023
The main goal of this work is the resolution offluid structure interaction problems described with the Lagrangian formalism by means of a consistently derived monolithic approach. The use of a component-free derivation leads to a straightforward implementation of the formulation where only vectors and second-order tensors in R3 are required. Therefore, no basis or components have to be imposed ab initio for the discrete variational formulation as occurs when Voigt notation is employed. The computational framework adopted is the local maximum-entropy material point method (LME-MPM), a mesh-free technique that combines the material point sampling of the MPM and the LME, a spatial approximation technique with basis functions of class C∞. This framework sidesteps the use of expensive mesh refinement techniques, which are typically required when Lagrangian finite element method is employed. Finally, the effectiveness of this approach is illustrated against challenging fluid dynamic problems.
@article{Molinos2023, author = {Molinos, Miguel and Chandra, Bodhinanda and Stickle, Miguel M and Soga, Kenichi}, doi = {10.1007/s00707-022-03459-1}, issn = {0001-5970}, journal = {Acta Mechanica}, number = {5}, pages = {1777--1809}, publisher = {Springer Vienna}, title = {{On the derivation of a component-free scheme for Lagrangian fluid–structure interaction problems}}, volume = {234}, url = {https://doi.org/10.1007/s00707-022-03459-1 https://link.springer.com/10.1007/s00707-022-03459-1}, year = {2023}, }
2022
- Shear band evolution and post-failure simulation by the extended material point method ( XMPM ) with localization detection and frictional self-contactYong Liang, Bodhinanda Chandra, and Kenichi SogaComputer Methods in Applied Mechanics and Engineering, Mar 2022
An enhanced XMPM formulation is proposed to simulate the evolution of shear bands and post-failure behaviors with large deformations. In the current study, a localization search algorithm based on the theory of bifurcation is integrated into the XMPM to predict the initiation and propagation of discontinuity. In addition, a formulation of self-contact is proposed to deal with the dynamic frictional contact mechanism between the generated shear planes. In order to ensure the smoothness of the discontinuity surface during localization propagation, a hybrid implicit–explicit description of discontinuity is assumed by employing the level-set method and a point cloud approach. Several numerical examples are investigated to assess the accuracy and demonstrate the capability of the proposed XMPM approach in simulating the shear band evolution of different engineering problems in both 2D and 3D. The proposed formulation also exhibits minor sensitivity with respect to mesh refinements in predicting the shear-band path. To show the optimum performance compared to the regular MPM approach, a simulation of large-deformation heterogeneous slope failure is presented as one of the applications of the proposed method towards simulating real-scale engineering problems.
@article{Liang2022, author = {Liang, Yong and Chandra, Bodhinanda and Soga, Kenichi}, doi = {10.1016/j.cma.2021.114530}, issn = {0045-7825}, journal = {Computer Methods in Applied Mechanics and Engineering}, keywords = {extended material point method,localization detection,shear band,strong discontinuity}, pages = {114530}, publisher = {Elsevier B.V.}, title = {{Shear band evolution and post-failure simulation by the extended material point method ( XMPM ) with localization detection and frictional self-contact}}, url = {https://doi.org/10.1016/j.cma.2021.114530}, volume = {390}, year = {2022}, }
2021
- A semi-implicit material point method based on fractional-step method for saturated soilShyamini Kularathna, Weijian Liang, Tianchi Zhao, and 3 more authorsInternational Journal for Numerical and Analytical Methods in Geomechanics, Mar 2021
In this paper, a new formulation ofmaterial point method (MPM) to model coupled soil deformation and pore fluid flow problems is presented within the framework ofthe theory of porous media. The saturated porous medium is assumed to be consisting of incompressible pore fluid and deformable soil skeleton made up of incompressible solid grains. The main difference of the proposed MPM algorithm is the implicit treatment of pore-water pressure which satisfies its incompressibility internal constraint. The resulting solid-fluid coupled equations are solved by using a splitting algorithm based on the Chorin’s projection method. The splitting algorithm helps to mitigate numerical instabilities at the incompressibility limit when equal-order interpolation functions are used. The key strengths of the proposed semi-implicit coupled MPM formulation is its capa- bility to reduce pressure oscillations as well as to increase the time step size, which is independent of the fluid incremental strain level and the soil permeability. The proposed semi-implicit MPM is validated by comparing the numerical results with the analytical solutions of several numerical tests, including 1D and 2D plane-strain consolidation problems. To demonstrate the capability of the proposed method in simulating practical engineering problems involving large deformations, a hydraulic process leading to slope failure is studied, and the numerical result is validated by the monitored data.
@article{Kularathna2021, author = {Kularathna, Shyamini and Liang, Weijian and Zhao, Tianchi and Chandra, Bodhinanda and Zhao, Jidong and Soga, Kenichi}, doi = {10.1002/nag.3207}, journal = {International Journal for Numerical and Analytical Methods in Geomechanics}, keywords = {fractional-step method,incompressible pore fluid,material point method,saturated soil,slope instability}, pages = {1--32}, title = {{A semi-implicit material point method based on fractional-step method for saturated soil}}, url = {https://doi.org/10.1002/nag.3207}, year = {2021}, } - Nonconforming Dirichlet boundary conditions in implicit material point method by means of penalty augmentationBodhinanda Chandra, Veronika Singer, Tobias Teschemacher, and 2 more authorsActa Geotechnica, Mar 2021
In many geomechanics applications, material boundaries are subjected to large displacements and deformation. Under these circumstances, the application of boundary conditions using particle methods, such as the material point method (MPM), becomes a challenging task since material boundaries do not coincide with the background mesh. This paper presents a formulation of penalty augmentation to impose nonhomogeneous, nonconforming Dirichlet boundary conditions in implicit MPM. The penalty augmentation is implemented utilizing boundary particles, which can move either according to or independently from the material deformation. Furthermore, releasing contact boundary condition, as well as the capability to accommodate slip boundaries, is introduced in the current work. The accuracy of the proposed method is assessed in both 2D and 3D cases, by convergence analysis reaching the analytical solution and by comparing the results of nonconforming and classical grid-conforming simulations. Keywords
@article{Chandra2021, author = {Chandra, Bodhinanda and Singer, Veronika and Teschemacher, Tobias and W{\"{u}}chner, Roland and Larese, Antonia}, doi = {10.1007/s11440-020-01123-3}, isbn = {1144002001}, journal = {Acta Geotechnica}, keywords = {implicit time integration,material point method,nonconforming boundary conditions,penalty method}, title = {{Nonconforming Dirichlet boundary conditions in implicit material point method by means of penalty augmentation}}, year = {2021}, } - Fluid–rigid-body interaction simulations and validations using a coupled stabilized ISPH–DEM incorporated with the energy-tracking impulse method for multiple-body contactsMitsuteru Asai, Yi Li, Bodhinanda Chandra, and 1 more authorComputer Methods in Applied Mechanics and Engineering, Mar 2021
In this paper, a new particle-based fluid–rigid-body interaction simulator for violent free-surface flow problems is developed. The incompressible Smoothed Particle Hydrodynamics (ISPH) method has been proven to produce a smooth and accurate pressure distribution of free-surface fluid flow with breaking and fragmentation. Computed hydrodynamic forces can be applied onto rigid bodies, which may simultaneously experience contact or impact with the surrounding wall boundaries or another rigid body. Modeled by using the discrete element method (DEM), the contact force between rigid bodies is traditionally calculated employing the penalty approach, where a spring-based repulsive force is approximated at the vicinity of contact points depending on the deepest penetration depth. However, for high-speed collision problems involving a system of many rigid bodies, the values of approximated repulsive forces may be highly overestimated, and thus, a much smaller time step and an excessive damping parameter are often required to stabilize the approximated forces. This problem is highly inefficient for the computational resources of the fluid–rigid body interaction simulation since the computational cost at each time step is mostly dominated by the incompressible fluid simulation. The capability to increase the time increment following the critical time step of the fluid solver is, therefore, strongly demanded to increase the simulation efficiency. The current paper incorporates the usage of the energy-tracking impulse (ETI) method as an alternative approach to handle contact accurately. To achieve better energy conservation and enhance stability, Stronge’s hypothesis is considered instead of the generally assumed Newton’s contact law. The current work also covers three experimental validation tests, which were conducted to assure the quality and robustness of the coupled ISPH–DEM implementation.
@article{Asai2021, author = {Asai, Mitsuteru and Li, Yi and Chandra, Bodhinanda and Takase, Shinsuke}, doi = {10.1016/j.cma.2021.113681}, issn = {00457825}, journal = {Computer Methods in Applied Mechanics and Engineering}, keywords = {Contact,Discrete Element Method,Fluid–structure interaction,Rigid-body dynamics,Smoothed Particle Hydrodynamics,Validation and verification}, title = {{Fluid–rigid-body interaction simulations and validations using a coupled stabilized ISPH–DEM incorporated with the energy-tracking impulse method for multiple-body contacts}}, volume = {377}, year = {2021}, }
2020
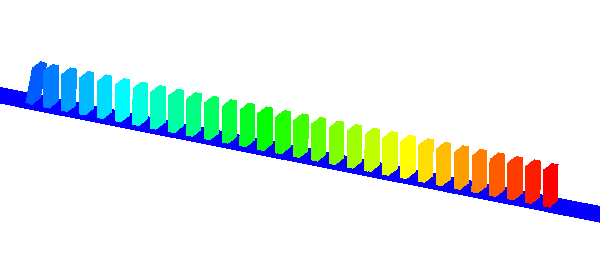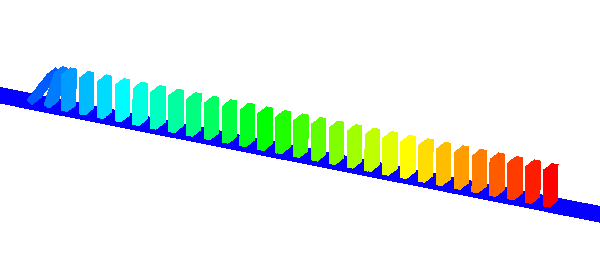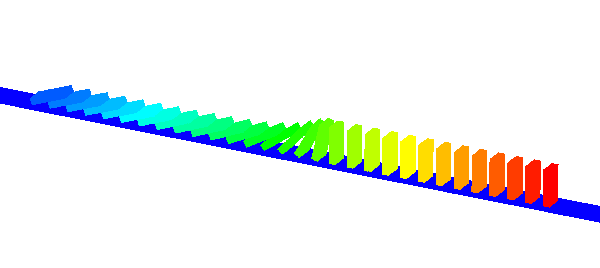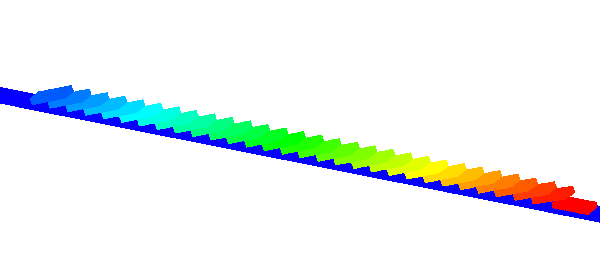
- Energy-tracking impulse method for particle-discretized rigid-body simulations with frictional contactYi Li, Mitsuteru Asai, Bodhinanda Chandra, and 1 more authorComputational Particle Mechanics, Mar 2020
Simulations of multi-body dynamics for computer graphics, 3D game engines, or engineering simulations often involve contact and articulated connections to produce plausible results. Multi-body dynamics simulations generally require accurate contact detection and induce high computational costs because of tiny time increments. As higher accuracy and robustness are continually being sought for engineering purposes, we propose an improved multi-body dynamics simulator based on an impulse method, specifically an energy-tracking impulse (ETI) algorithm that has been modified to handle particle-discretized rigid-body simulations. In order to decrease the computational costs of the simulations, in the current work, we assume a fixed moderate time increment, allowing multiple-point contacts within a single time increment. In addition to that, we distinguish the treatment between point-to-point and multiple-point contacts, which include edge-to-surface and surface-to-surface contacts, through an additional sub-cycling iterations. The improved ETI method was verified with analytical solutions of examples with single-body contact, a frictional slip, and a rolling contact. Moreover, the method was also validated with an experimental test of a line of dominoes with multiple-point contacts. Finally, a demonstration simulation with bodies of complicated shape subjected to a large number of constraints is given to show the optimum performance of the formulation.
@article{Li2020, author = {Li, Yi and Asai, Mitsuteru and Chandra, Bodhinanda and Isshiki, Masaharu}, doi = {10.1007/s40571-020-00326-5}, isbn = {4057102000}, issn = {21964386}, journal = {Computational Particle Mechanics}, keywords = {Contact,Impulse method,Multi-body dynamics,Particle method}, pages = {237--258}, title = {{Energy-tracking impulse method for particle-discretized rigid-body simulations with frictional contact}}, year = {2020}, }
